Opmerkingen bij kadering statistische resultaten van de Grote Coronastudie
Inleiding
Enkele weken geleden hebben Thomas Neyens (UHasselt & KU Leuven), Jonas Crèvecoeur (UHasselt & KU Leuven), Niel Hens (UHasselt & UAntwerpen), Geert Molenberghs (UHasselt & KU Leuven), Koen Pepermans (UAntwerpen), Jan Aerts (UHasselt), Pierre Van Damme (UAntwerpen), Philippe Beutels (UAntwerpen) een lang verwachte kadering van de statistische resultaten van de Grote Coronastudie (GCS) gepubliceerd.
De eerste bladzijden lezen als een beknopte inleiding in kwantitatieve onderzoeksmethoden. Alleen daarom al, loont het de moeite om het stuk van Neyens, Crèvecoeur, Hens et al. (2021) te lezen. Met name voor niet-specialisten is dit zeer lezenswaardig. De auteurs slagen er in om in enkele paragrafen en in een eenvoudige taal wegwijs te maken in de verschillende onderzoeksmethoden.
Daarna wordt de GCS in dit kader geplaatst en van naderbij bekeken. Samengevat is de GCS is een observationele, niet-probabilistische survey die cross-sectioneel gebruikt wordt en zowel een samenvattend als een comparatief oogmerk heeft.
Het zal voor veel lezers duidelijk zijn dat het meest problematische van deze opzet het niet-probabilistisch karakter van de studie is. Concreet wil dat zeggen dat deelnemers zelf het initiatief nemen om deel te nemen. De vertekening die hiermee gepaard gaat wordt in de GCS gecorrigeerd door een weging op geslacht, leeftijd, opleidingsniveau en residentiële provincie.
In het tweede deel doen de auteurs hun best om te illustreren dat, ondanks de gebreken van niet-probabilistische studies, de GCS toch waardevolle informatie kan opleveren. Ze doen dat door te verwijzen naar de brede oproepen die ze gedaan hebben op de klassieke media en de betaalde reclame waarvan ze gebruik hebben gemaakt op de sociale media. Ze wijzen (terecht) op het feit dat de GCS beschikbaar is in vier talen (Nederlands, Frans, Duits en Engels). Verder verwijzen ze naar het feit dat de resultaten vaak worden vermeld in de media waardoor veel mensen zich bewust zijn van de studie. Uiteraard wordt het heel grote aantal deelnemers vermeld. Initieel was dat meer dan een half miljoen deelnemers. Nu schommelt het tussen de 20,000 en de 35,000.
Neyens, Crèvecoeur, Hens et al. (2021) besluiten dan ook dat ze “ervan overtuigd zijn dat deze studie, ondanks gebruikelijke studiebeperkingen, van grote waarde is, niet enkel als gegevensbron voor de wetenschappelijke wereld, maar ook als tool die de beleidsvorming kan helpen door snel tendensen en signalen op te vangen”.
Kritische evaluatie
Mijn mening is iets genuanceerder. Ik denk dat het goed is dat we over de GCS kunnen beschikken, al is het maar omdat we over weinig andere alternatieven beschikken. Maar na meer dan een jaar had men toch aan beter instrument kunnen werken. Enkele weken geleden was er weliswaar een initiatief van, o.a., Statistiek Vlaanderen waarin wel een toevalssteekproef werd gebruikt, maar dat was enkel voor Vlaanderen. Overigens, heb ik tot mijn verbazing moeten vaststellen dat deze studie veel minder media aandacht heeft gekregen dan, bijvoorbeeld, de GCS.
Selectie vertekening
Ook al halen de auteurs selectie vertekening of selection bias aan, toch wordt er vrij snel om het probleem gewalst. In deze paragraaf proberen we alvast één bijkomend probleem aan kaarten. We gebruiken hiervoor een vereenvoudigde, fictieve, probleemstelling, kwestie van het overzichtelijk te houden. Voor een algemeen overzicht van selection bias bij web surveys verwijs ik naar Bethlehem (2010).
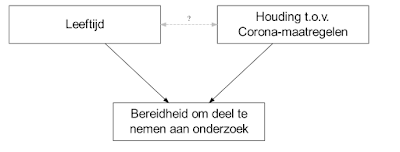
Stel dat we willen weten in welke mate de Belgische bevolking achter de Corona-maatregelen van het regeringscomité staat. We hebben een hypothese dat leeftijd daarin geen rol speelt, en we willen nagaan of onze hypothese wel klopt. We zijn dus geïnteresseerd in de mate waarin mensen achter de Corona-maatregelen staan, en het verband tussen die variabele en leeftijd. Bovendien weten we de exacte verdeling van de variabele leeftijd voor de ganse populatie. We gebruiken die gegevens om te wegen, net zoals de GCS dat ook doet. De GCS weegt niet enkel op leeftijd, maar ook op geslacht, opleidingsniveau en residentiële provincie. De redenering achter weging van GCS samen met een eenvoudig voorbeeld vind je terug in de paragraaf Samenvattende statistische analyse op p. 6-7 van Neyens, Crèvecoeur, Hens et al. (2021). We doen dit omdat we uit ervaring of ander onderzoek weten dat, bijvoorbeeld, jongeren minder bereid zijn om mee te werken aan wetenschappelijk onderzoek. In de realiteit is het verband tussen leeftijd en de mate waarin men meewerkt met onderzoek veel complexer. Stel je nu voor dat de houding ten opzichte van de Corona-maatregelen van de regeringen ook een invloed heeft op het deelnemen aan de GCS. Opnieuw, in de realiteit zijn dergelijke verbanden complexer, maar voor de eenvoud van deze illustratie gaan we ervan uit dat er een positief verband tussen houding ten opzichte van de Corona-maatregelen en bereidheid tot deelname. Dit lijkt bij de haren getrokken, maar er zijn genoeg voorbeelden uit de sociaal-wetenschappelijke literatuur die op zo'n verband wijzen. Bemerk overigens dat bij de Motivatiebarometer van de Universiteit van Gent er al expliciet in de fout wordt gegaan door op de landingspagina uit te pakken met een boodschap van de eerste minister. Voor alle duidelijkheid. Ik steun de eerste minister en z’n campagnes, maar dit hoort niet thuis in een objectief meetinstrument.
Schematisch kunnen we de hierboven geschetste situatie als volgt voorstellen (Voor meer details over deze notatie zie Pearl & Mackenzie (2019) en Thoemmes & Mohan (2015).):
Vervolgens heb ik een steekproef van 10,000 eenheden genomen waarbij de selectiekans afhangt van leeftijd en de houding t.o.v. de Corona maatregelen. In die steekproef is de gemiddelde leeftijd bijna 10 jaar ouder (67.6 jaar) dan in de populatie waar ze uit getrokken is. Dat hoeft niet te verbazen, gegeven de selectiemethode die gehanteerd is. We merken trouwens op dat na weging de gemiddelde leeftijd terug daalt naar 58.8, zeer dicht bij de populatie-waarde. Laat ons dan eens kijken naar de gemiddelde score op de 10-punten schaal van mate waarin men achter de Corona-maatregelen van het regeringscomité staat. Deze bedraagt 6.2 in de steekproef. Dat is bijna een kwart meer dan het gemiddelde in de populatie waaruit de steekproef genomen is. Ook dat hoeft niet te verbazen gegeven dat we een verband hebben verondersteld tussen leeftijd en bereidheid tot deelname aan dit soort van onderzoek.
Wat vervelender is, is dat, na weging, dit gemiddelde nagenoeg hetzelfde blijft of zelfs iets stijgt (6.4). Meer nog, daar waar in de populatie de correlatie tussen leeftijd en de mate waarin men achter de Corona-maatregelen van het regeringscomité staat 0 was, bedraagt die correlatie nu -0.18. Dit is, bij zo'n grote steekproef, overigens significant. Ook hier helpt wegen niet (correlatie bedraagt dan -0.21). Dit verschijnsel is een illustratie van wat soms de paradox van Berkson wordt genoemd. De epidemiologen en bio-statistici onder de auteurs kennen deze paradox maar al te goed, maar men had volgens mij duidelijker moeten verwoorden dat de assumptie wordt gemaakt dat er in de GCS geen enkele van dergelijke variabelen bestaan. Persoonlijk denk ik overigens dat zo'n assumptie niet realistisch is in deze context. Overigens verscheen onlangs nog een overzichtsartikel over collider bias in de context van COVID-19 (zie Griffith, Morris, Tudball et al., 2020).
Het punt hier is niet dat leeftijd een effect heeft op deelnamebereidheid, dat weten we al. Ik probeer wel te illustreren dat er heel wat variabelen denkbaar zijn die die rol kunnen spelen en dat weging in dat geval weinig aan het probleem verhelpt. Dit had in Neyens, Crèvecoeur, Hens et al. best wat explicieter naar voren mogen worden geschoven.
Comparatieve statistische analyse
De auteurs stellen dat (Neyens, Crèvecoeur, Hens et al., 2021, p. 7):
Vergelijkingen doen we via statistische modellen. In die modellen hebben niet-representatieve steekproeven meestal geringe effecten wanneer de karakteristieken die vertekening veroorzaken als zogenaamde confounders in de modellen opgenomen worden.
De vraag is natuurlijk of die mogelijke confounders op afdoende wijze zijn gemeten in de vragenlijst en vervolgens zijn opgenomen in statistische modellen. Het is, bijvoorbeeld, helemaal niet zo'n gekke hypothese om te veronderstellen dat de houding van mensen ten opzichte van de Corona-maatregelen voor een deel te maken hebben met de algemene politieke en ideologische houding van mensen. Voor zover ik weet werd dit niet gemeten in de GCS.
Het probleem van niet gemeten confounders geldt natuurlijk ook voor onderzoek dat gebaseerd is op een representatieve steekproef. Het punt is hier eerder dat de auteurs expliciet het opnemen van confounders vermelden als voorwaarde voor het maken vergelijkingen bij niet-representatieve steekproeven. Met andere woorden, de assumptie hier is dat alle mogelijke, belangrijke, confounders zijn gemeten in de GCS en vervolgens zijn opgenomen in de statistische modellen.
Terloops wil ik hierbij opmerken dat, in de context van houdingen en gedragingen gemeten via zelf-rapportering, de richting van causale verbanden niet altijd éénvoudig vast te stellen is. Een confounder kan dan eigenlijk een collider blijken te zijn en in dat geval kan je de variabele beter niet opnemen in je statistisch model (Zie McElreath, 2020).
Hoe dan ook, de auteurs geven, mijns inziens, een te optimistisch beeld van de mate waarin statistische modellen in staat zijn om uit niet-representatieve steekproeven zoals de GCS toch correcte vergelijkingen te maken. Het probleem ligt voornamelijk bij de niet-geobserveerde determinanten van de variabelen waarin we interesse hebben. Mijn bekommernis richt zich voornamelijk op het gedeelte van de studie dat gaat over de publieke opinie rond Covid en de regeringsmaatregelen. Ik laat dus wel de mogelijkheid open dat de data van de GCS nuttig kan zijn om het verloop van de epidemie te modelleren. Ik ga er immers van uit dat die modellen expliciet rekening houden met de vertekeningen die zich bij niet-representatieve steekproeven kunnen voordoen.
Vertekening-variantie afweging
Vertekening-variantie afweging, beter bekend onder de Engelse benaming Bias–variance tradeoff, verwijst naar het conflict dat ontstaat door te proberen twee soorten fouten, bias en variantie, te minimaliseren. Concreet wil dit bij de GCS zeggen dat men weging op geslacht, leeftijd, opleidingsniveau en residentiële provincie gebruikt als middel om bias te reduceren (bij routinematige rapporten). De auteurs geven toe dat dit problematisch is voor bepaalde groepen. Zo zijn er relatief weinig laaggeschoolde, oudere mannen uit Henegouwen in de steekproef, wat de precisie doet dalen. Dit verwijst naar de variantie component van de bias-variantie afweging. De oplossing die de GCS daarvoor hanteert is het aftoppen van gewichten zodat een gewicht maximaal 40 keer zo groot kan zijn als het kleinste gewicht.
Het criterium van 40 wijst erop dat bepaalde groepen zoals mannelijke, oudere, laagopgeleide inwoners van Henegouwen verschillende malen minder vaak voorkomen dan je zou verwachten op basis van de populatie. Het exacte aantal keren kan ik niet afleiden uit het getal 40, maar ik vermoed dat het groter is dan 5 keer. Aftoppen op zich is zeker verdedigbaar, maar je zou dan wel explicieter mogen stellen dat je de variantie reductie betaalt door een verhoogde bias. Je kan je de vraag stellen wat in de GCS primeert, bias of variantie. Mij lijkt het dat voor heel wat rapporten en kerncijfers die uit de GCS worden afgeleid, bias belangrijker is dan variantie. Laat me deze stelling illustreren door terug te grijpen naar de vraag in welke mate de Belgische bevolking achter de Corona-maatregelen van het regeringscomité staat. Als we niet over een wetenschappelijk instrument beschikken om dit te meten kunnen we alleen maar gissen op basis van wat er in de kranten geschreven wordt, wat op de sociale media te lezen is of wat onze vrienden en collega's te vertellen hebben. Ik denk dat iedereen het over eens zal zijn dat dit geen goede alternatieven zijn. De GCS zou, voor deze vraagstelling, zich moeten concentreren op de vraag of het percentage voorstanders, ik zeg maar wat, 25%, 50% of eerder 75% is. M.a.w. staat de meerderheid erachter, of slechts een minderheid, of is het een dubbeltje op z'n kant? In dat geval zijn we minder geïnteresseerd of er nu rond die schatting een betrouwbaarheidsinterval van, ik zeg opnieuw maar wat, 2%, 4% of 8% breed is. Uiteraard is een kleiner betrouwbaarheidsinterval beter, maar in dit gevoelig thema, waarin de zwijgende meerderheid zelden gehoord wordt, lijkt bias me erger.
Ik wil hier wel opnieuw een uitzondering maken voor het gedeelte van de GCS dat gebruikt wordt om de statistische modellen die gebruikt worden op het verloop van de pandemie te voorspellen. Voor deze modellen is variantie allicht wel belangrijker dan voor de meer algemene rapportering rond maatschappelijke thema's. De auteurs verwijzen trouwens naar specifieke, en vaak vernieuwende, technieken die hiervoor werden gebruikt.
Alternatieven
Zijn er dan geen alternatieven? Die zijn er wel. Het meest evidente alternatief is de toevalssteekproef. Als er één toestand is waarbij vrijwel iedereen het ermee eens zal zijn dat het trekken van een toevalssteekproef uit het Rijksregister geoorloofd is dan is het deze wel. De Corona-crisis is allicht de grootste crisis waar België tegenaan kijkt sinds de tweede wereldoorlog. Het is van cruciaal belang om te weten wat de houdingen zijn van mensen rond deze crisis. Het is van cruciaal belang om dat dan ook op een wetenschappelijk correcte manier te doen. Bovendien lijkt deze Corona-crisis de mogelijkheid bij uitstek om een goede respons te halen. Zowat iedereen, zowel de voorstanders van strenge maatregelen als de tegenstanders daarvan, hebben belang bij een correct meting. Een goed georchestreerde campagne, met zowel voor als tegenstanders, rond het belang van deelname aan zo'n onderzoek zou in mijn ogen een historische responsegraad kunnen opleveren.
Toegegeven, in zo'n geval zou je niet de grote steekproef aantallen halen waar de GCS over kan buigen. Ik ben er me ook bewust van dat die grote aantallen van belang zijn van zodra men ook geografische verschillen wil meten. Ik vermoed dat dit vooral voor de modellen belangrijk is. Hoe dan ook, ik vind het een gemiste kans dat men niet minstens één van de GCS edities heeft laten samengaan met een landelijke, op het Rijkregister gebaseerde, studie. Als men dan een aantal gemeenschappelijke vragen had opgenomen had men over vergelijkingsmateriaal beschikt dat vanuit wetenschappelijk en beleidsstandpunt bijzonder waardevol was geweest. Gegeven de gigantische kost die de overheid moet dragen in deze Corona-crisis is deze kost peanuts. Als uit zo'n vergelijking zou blijken dat de GCS het best aardig doet, dan zou dat sceptici zoals ikzelf over de streep kunnen trekken.
In de survey literatuur worden overigens ook een aantal alternatieven voorgesteld. Graag verwijs ik naar een methode die Multilevel Regression and Post-stratification (MrP) wordt genoemd. In die methode wordt poststratificatie gebruikt om te corrigeren voor selection bias, ook al is de vertekening groot en zijn er veel (combinaties van) variabelen in betrokken. Multilevel regressie wordt dan weer gebruikt om te zorgen voor stabiele schattingen op kleine subgroepen. Voor meer details zie Wang, Rothschild, Goel and Gelman (2015).
Een gekend voorbeeld is dat van een panel van xbox-gebruikers in de Verenigde Staten dat werd bevraagd over hun voorkeur voor twee presidentskandidaten. Zo'n panel is bij uitstek niet-probabilistisch en gebiased. Het panel heeft een oververtegenwoordiging van jongeren, mannen en blanken. Toch bleek dat de analyse met de MrP-methode goede resultaten opleverden (Wang, Rothschild, Goel and Gelman, 2015).
De steekproef van de GCS is natuurlijk niet zo zwaar gebiased als deze van de xbox gebruikers, maar het toepassen van dergelijke methoden zou volgens mij ook voor de GCS vruchtbaar kunnen zijn.
Beleidsconsequenties
Mijn conclusie is dat het goed is dat de GCS bestaat. Het heeft z'n dienst bewezen in moeilijke tijden. Maar, naar analogie met het Deltaplan dat na de overstromingsramp van 1953 in Nederland werd opgezet om ervoor te zorgen dan een dergelijke ramp zich niet nogmaals zou kunnen voltrekken, heeft België, m.i., nood aan een sociaal-wetenschappelijk Deltaplan waarin, op een rigoureus wetenschappelijke manier, op geregelde tijdstippen, naar de houdingen van de Belgen t.o.v. belangrijke maatschappelijke thema's wordt gepeild. Bij afwezigheid van een dergelijk meetinstrument wordt het maatschappelijk debat te veel gekleurd door de hardste roepers op de sociale media. De afgelopen anderhalf jaar hebben we te vaak regeringen zien zwichten voor de druk waarbij, m.i., de stem van de stille meerderheid over het hoofd werd gezien.
Referenties
Bethlehem, J. (2010). Selection bias in web surveys. International Statistical Review, 78(2),
161-188. https://doi.org/10.1111/j.1751-5823.2010.00112.x
Griffith, G.J., Morris, T.T., Tudball, M.J. et al. (2020). Collider bias undermines our understanding of COVID-19 disease risk and severity. Nat Commun 11, 5749. https://doi.org/10.1038/s41467-020-19478-2
McElreath, R (2020). Statistical Rethinking. A Bayesian Course with Examples in R and Stan. Second Edition. Boca Raton: CRC Press.
Neyens, T, J. Crèvecoeur, N. Hens, G. Molenberghs, K. Pepermans, J. Aerts, P. Van Damme, P. Beutels (2021). De Grote Coronastudie: een kadering van statistische resultaten. In: https://covid-en-wetenschap.github.io/2021/04/grote-coronastudie-kadering.
Pearl, J. and D. Mackenzie (2019). The Book of Why: The New Science of Cause and Effect. Penguin
Thoemmes, F. and K. Mohan (2015). Graphical Representation of Missing Data Problems. Structural Equation Modeling: A Multidisciplinary Journal, 22: 631–642, 2015
Wang, W., D. Rothschild, S. Goel, A. Gelman (2015). International Journal of Forecasting, 31(3), 980-991. Elsevier.


Comments
Post a Comment